header_image
A recent Twitter hack lead to many verified Twitter accounts being hijacked, including Elon Musk, Bill Gates, Barack Obama, and even presidential candidate Joe Biden. The accounts soon started posting 'doubling bitcoin' scams - reminiscent of the age old 'doubling gp' scam in the game Runescape. Send me some money, and I'll send you double back! 🤑

elon

<!---The hacker, who had the ability to impersonate the most powerful people on the planet, only managed to steal ~$120,000 USD. There has been great confusion as to why the hacker with such unrestricted power would go with such a poor scam. Much speculation has arisen, with a few predominant themes: 1. The hacker panicked upon gaining their access. The hacker may have believed they had a small window of time before they lost access to the accounts, and thus went with the easiest scam they could think of. 2. The hacker had no other capital to invest into a more profitable scam. While more elaborate and perhaps riskier, the hacker could have tweeted in such a way to crash stocks or even entire markets given the enormity of their power. For example, Elon Musk's [tweets in the past](https://www.washingtonpost.com/technology/2020/05/01/musk-tesla-stock/) have reduced Tesla's share price by more than 10 percent. * If the hacker was concerned about traceability with stock trades, they could have just opened a highly leveraged anonymous position on bitcoin and posted bullish statements such as "We should look towards moving the United States to a Bitcoin standard dollar". I believe this would have been far more profitable and also less bad publicity for Bitcoin 😏, though it would require some initial capital. 3. This was not the real hack, but possibly a diversion away from something greater. It is currently unconfirmed as to whether the hacker had access to the private messages on the accounts they had accessed. If this data has been stolen, there is great potential for large scale blackmail using the private conversations between verified celebrities, journalists, politicians etc. Currently the cause of the hack is being described as social engineering, where Twitter has stated that at lease one of its employees is involved. --->

A Message to the Hacker

A 0.00121639 BTC (~$12 USD) bitcoin transaction to the hacker's address was made sometime after the hack, containing a hidden message. The transaction involved seven outputs, one output directed to the attacker's address, and six outputs directed to customised vanity addresses:

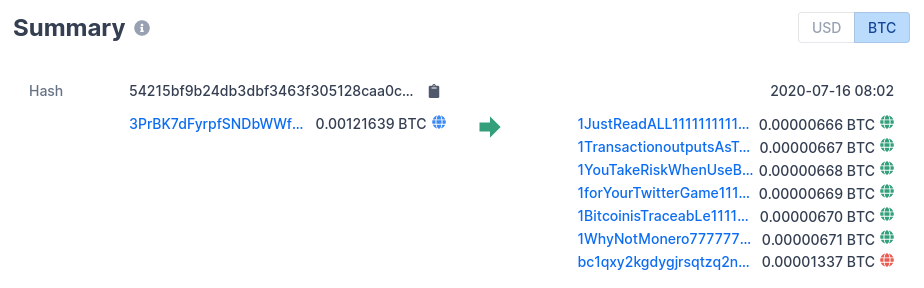
transactions

Here we see a message encoded in the 6 customised vanity addresses:

Just Read All
Transaction Outputs As Text
You Take Risk When Use Bitcoin
For Your Twitter Game
Bitcoin is Traceable
Why Not Monero

Monero is a privacy coin that uses an obfuscated ledger where it is impossible to determine the source, amount, or destination of transactions. Whereas Bitcoin transactions are fully transparent and hence pseudo-anonymous as long as your addresses are detached from your identity. Information can be gathered about a particular Bitcoin address by following bitcoin transactions in the blockchain.

It appears that someone decided to give the hacker some advice: use Monero for these scams or else you risk getting caught. While it is difficult to ascertain exactly what the messager is saying, it is likely they are suggesting the hacker exchange their stolen bitcoin for monero, so that the transaction trail is lost. It would be a poor choice to replace "doubling bitcoin" scams with "doubling monero" scams, as attempting to scam Monero would dramatically reduce the already tiny 'target audience' for the attack:

target audience

The Improbable Vanity Address

The probability of generating a Bitcoin vanity address like 1YouTakeRiskWhenUseBitcoin11cGozM, which contains 25 sequential desired characters, is roughly $$ (1/58)^{25} $$. The 58 comes from Bitcoin's usage of base58, where there are 58 possible characters to choose from (numbers, lowercase & uppercase letters except for 0/O/I/l as these are easily mistaken).

It would take an average of $$ \sim 1.218\times10^{44} $$ addresses to be generated before finding an address that matches this desired pattern. A fast vanity address generator running on a modern GPU can create approximately 500 million addresses per second ($$ 5\times10^{8} $$), meaning it would take approximately $$ 2.56\times10^{35} $$ seconds, or $$ 5.8\times10^{17} $$ universes of time. This is an impossibly long time. So how did they do it and not just once, but for 6 vanity addresses?

Whose Address is it Anyway?

There is no 'registration' of addresses in Bitcoin, private keys and corresponding addresses can be generated entirely offline. This means that you can send bitcoin to an address that does not necessarily have an owner who has a corresponding private key, provided the address satisfies a few requirements.

The address format used by the message sender was 'legacy' P2PKH implimented by Satoshi Nakamoto. These addresses look like 1NcEUAqEqni2m6sUugSfEi8cSHbUqmi3xZ and involve three main requirements:

  1. The address begins with a 1 to signify this is a mainnet address and not a testnet address.
  2. The address is 25-34 characters in length. Most are 33-34 characters long.
  3. The address has a valid checksum.

P2PKH Technical Details (can skip over, 4 & 5 relevant)

For a complete tutorial on how this works, please see https://nickfarrow.com/Cryptography-in-Bitcoin-with-C/.

With a public_key=0250863ad64a87ae8a2fe83c1af1a8403cb53f53e486d8511dad8a04887e5b2352:

  1. Calculate the SHA-256 hash of the public key
  2. Calculate the RIPEMD-160 hash of this SHA-256 hash
  3. Add a version byte in front of this to complete our address (0x00 for main-net)
  4. To create a checksum we take the SHA-256 of this extended RIPEMD-160 hash twice and take the first 4 bytes
  5. Add the checksum to the end of the original RIPEMD160 hash at step 3
  6. Convert the byte result from hexidecimal into a base58 string
  7. Remove any extra leading 1's. In base58 a '1' represents a value of zero and thus has no value at the front of address. However, a leading '1' is included for each leading 00 byte.

Checking the Checkum

byte Explainer

The checksum is the last few digits of the address and allows anyone to confirm that an address is a legitimate address. If someone sends us an address, we can verify by performing steps 4 & 5 on the first 21 bytes, and then check that the last 4 bytes of the address match the rest of the address. This is most useful when entering a public address by hand where most wallets will prevent you from attempting to send bitcoin to an illegitimate address.

Faking Vanity

OK, so it would be impossible to create a vanity address this long legitimately. But can we fake one? Even though we will not have the private key to this address, and the bitcoin recieved will be unspendable, can we forge these addresses in order to send a message?

Well, the checksum also means it is very difficult to enter 33-34 characters and for the checksum requirements to be satisfied. Infact, given there are 4 bytes (32 bits) dedicated to the checkum, there is a $$ (1/16)^8 = (1/2)^{32} $$ chance or $$ 1 $$ in $$ 4,294,967,296 $$ of the checksum matching the other 21 bytes.

This could be brute forced, by designing a ~30 character long message and randomly trying a few billion combinations of the last characters would work, but very very slowly.

Forging an Address with C

There is a smarter way to create a crazy address like 1YouTakeRiskWhenUseBitcoin11cGozM. We can forge one. This will involve:

  1. Decide upon the text we wish to include in our address.
  2. Pad the address up to 33 characters.
  3. Convert this base58 address back into bytes.
  4. Recalculate the checksum from the first 21 bytes, and use it to overwrite the last 4 bytes.
  5. Converte the address bytes back to base58 format.

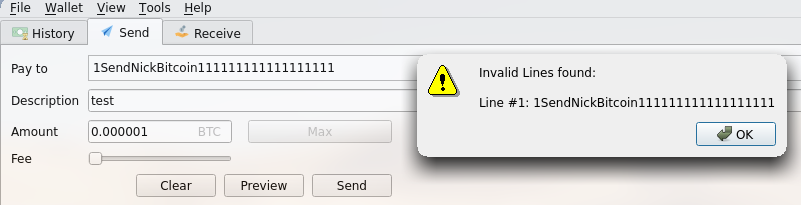
Some steps here will use some C programming, I'll try not to make it too technical. First we will choose our desired message, I'll go with SendNickBitcoin.

Next, we will put this into a format that resembles a bitcoin address,

We will not be able to send bitcoin to this address as it has an invalid checkum.
Failed Send

Next, we can convert this address back from base58 representation into bytes. For convenience I use learnmeabitcoin.com's base58 converter:
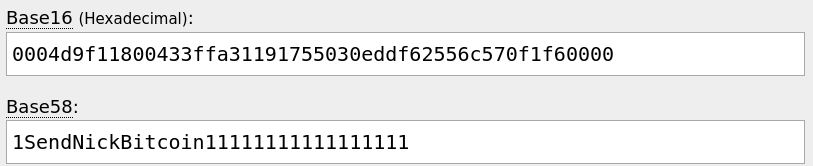
base58 decode

Now we have bytes 0004d9f11800433ffa31191755030eddf62556c570f1f60000. We can split this up into three parts:

From here we can recalculate the correct checksum for the version byte and public point (21 bytes), as in Step 4 of generating an address.

We can do this with some basic C. Here we are defining an unsigned char array with our bytes; setting up: 

#include <stdio.h>
#include <string.h>
#include <openssl/sha.h>

int main() {
        unsigned char custom_address[] = {
                0x00,
                0x04,
                0xd9,
                0xf1,
                0x18,
                0x00,
                0x43,
                0x3f,
                0xfa,
                0x31,
                0x19,
                0x17,
                0x55,
                0x03,
                0x0e,
                0xdd,
                0xf6,
                0x25,
                0x56,
                0xc5,
                0x70,
                0xf1,
                0xf6,
                0x00,
                0x00,
        };
}

You can get an easily copy-pastable list of bytes using these two lines of Python:

s = "0004d9f11800433ffa31191755030eddf62556c570f1f60000"
[print("0x{},".format(s[idx:idx+2])) for idx,val in enumerate(s) if idx%2 == 0]

Now we need to recalculate the checksum, and replace the final 4 bytes of custom_address. Inserting these lines into our main function:

    /* Declare a new unsigned char array to store the checksum bytes */
        unsigned char chksum[4];

        /* Calculate the checksum and store it in the checksum array */
        memcpy(chksum, SHA256(SHA256(custom_address, 21, 0), SHA256_DIGEST_LENGTH, 0), 4);

        /* Remembering the four bytes 22-25 at the end of our address are the checksum */
    /* Replace the existing, incorrect checksum with the new correct checksum */
        memcpy(custom_address+21, chksum, 4);

        /* Print the new address one byte at a time */
        int j;
        for (j = 0; j < 25; j++) {
                printf("%02X", custom_address[j]);
        }
        printf("\n");

Saving as fakeAddr.c, compiliing with gcc fakeAddr.c -o faker -lcrypto and running ./faker

$ ./faker
0004D9F11800433FFA31191755030EDDF62556C5707870A0CC

Now copy pasting into the base 58 encoder:
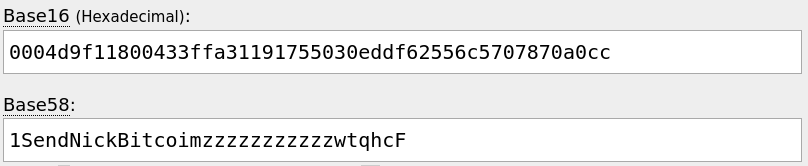
fake address base58

Pretty good! But not perfect. Sometimes the conversion back to base58 'carries over' (think division remainders) and changes the end. Let's try padding slightly differently with 7s instead of 1s like the messenger did with their final address. Our initial address as 1SendNickBitcoin77777777777777777:

$ ./faker
0004D9F11800433FFA3119175646962FB9CCCA97003FB0CC31

And converting to base58:
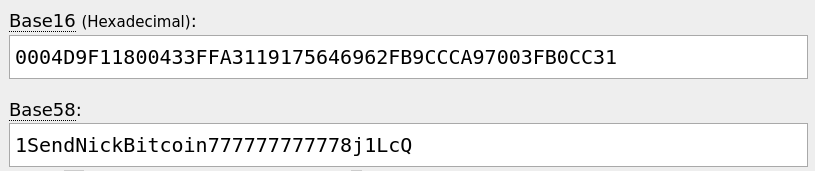
better fake address

Much better! Let's check we can send to the address. I'm going to do this on Bitcoin Cash because the transaction fees are cheap for testing.
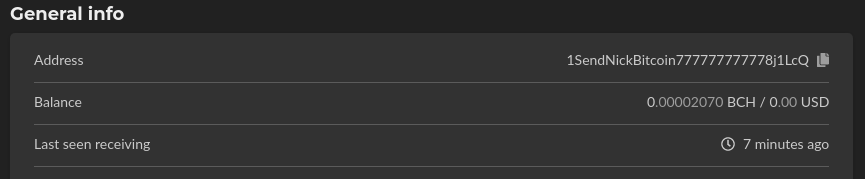
proof

The proof is in the blockchain, see it for yourself.

This method, or a slight variation of, is how someone encoded a hidden message in bitcoin transactions, to send to the Twitter hacker.

If you found this useful, please consider supporting me in creating these tutorials:

BTC: bc1qhyew3uytqkgkwr3zdfy98pcf982swlyukrk4tn

PLEASE do not send bitcoin to any other address in this post, it will be lost, and I will be very angry that you've sent bitcoin to an address I just explained as forged and unspendable.